Darcy-Weisbach Gleichung
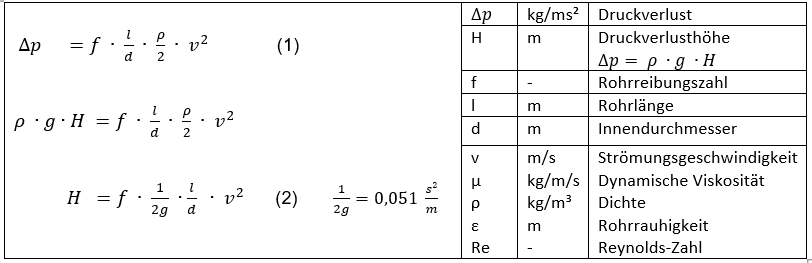 Die Gleichung nach Darcy-Weisbach ist ein empirischer Ansatz zur Berechnung von Druckverlusten der reibungsbehafteten Strömung
in geraden offenen Gerinnen und Rohrleitungen.
Ihr Charme liegt in der einfachen Anwendung. [Navier 1822] bietet mit seinem Differentialgleichungssystem einen analytischen Ansatz.
Leider lässt sich das Gleichungssystem nur für wenige Sonderfälle integrieren und wird in der Hauptsache mit
speziellen Computerprogrammen iterativ gelöst. Im Ingenieuralltag hat sich daher die Gleichung von Darcy-Weisbach durchgesetzt.
Tabelle 1 zeigt Ansätze bedeutender Autoren der ersten Hälfte des 19. Jahrhunderts zum Thema Druckverlust
in geraden Rohrleitungen bei turbulenter Wasserströmung. Die Formeln wurden empirisch aus Versuchen mit Rohren aus
Eisen und Gusseisen gewonnen.
Die Gleichung nach Darcy-Weisbach ist ein empirischer Ansatz zur Berechnung von Druckverlusten der reibungsbehafteten Strömung
in geraden offenen Gerinnen und Rohrleitungen.
Ihr Charme liegt in der einfachen Anwendung. [Navier 1822] bietet mit seinem Differentialgleichungssystem einen analytischen Ansatz.
Leider lässt sich das Gleichungssystem nur für wenige Sonderfälle integrieren und wird in der Hauptsache mit
speziellen Computerprogrammen iterativ gelöst. Im Ingenieuralltag hat sich daher die Gleichung von Darcy-Weisbach durchgesetzt.
Tabelle 1 zeigt Ansätze bedeutender Autoren der ersten Hälfte des 19. Jahrhunderts zum Thema Druckverlust
in geraden Rohrleitungen bei turbulenter Wasserströmung. Die Formeln wurden empirisch aus Versuchen mit Rohren aus
Eisen und Gusseisen gewonnen.
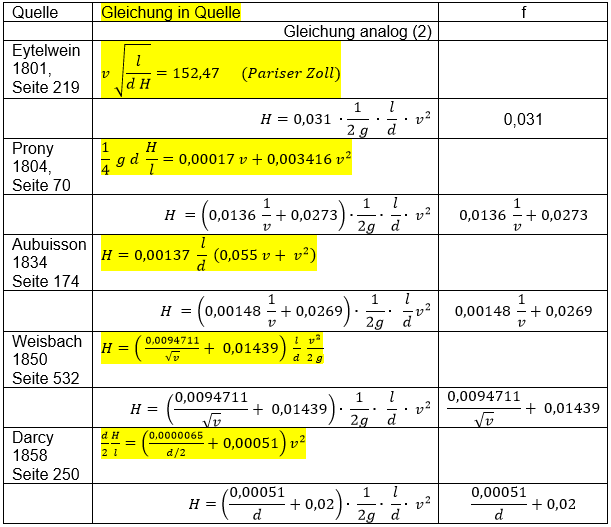 Tabelle 1
[Weisbach 1850, Seite 529] schrieb Gleichung (1) wie sie heute geläufig ist. Die Rohrreibungszahl f in Tabelle 1
wird durch die Einheiten der Konstanten dimensionslos.
Eytelwein zeigt einen Ansatz mit konstanter Rohrreibungszahl.
Weisbach´s Verständnis der Rohrreibungszahl f gleicht im Grundsatz dem von Prony und Aubuisson: f nimmt mit zunehmender
Strömungsgeschwindigkeit ab. Darcy arbeitet die Abhängigkeit der Rohrreibungszahl vom Rohrdurchmesser bei
gleichbleibender Rohrwandgüte (Rohrrauhigkeit) heraus. Beide Beobachtungen sind zutreffend. Auch die absoluten Werte
von f bewegen sich in der heute akzeptierten Größenordnung, wie ein Vergleich mit dem Diagramm nach Moody zeigt.
Colebrook formuliert hier die Rohrreibungszahl mit den dimensionslosen Größen (Rohrrauhigkeit/Durchmesser) und Reynoldszahl.
Tabelle 1
[Weisbach 1850, Seite 529] schrieb Gleichung (1) wie sie heute geläufig ist. Die Rohrreibungszahl f in Tabelle 1
wird durch die Einheiten der Konstanten dimensionslos.
Eytelwein zeigt einen Ansatz mit konstanter Rohrreibungszahl.
Weisbach´s Verständnis der Rohrreibungszahl f gleicht im Grundsatz dem von Prony und Aubuisson: f nimmt mit zunehmender
Strömungsgeschwindigkeit ab. Darcy arbeitet die Abhängigkeit der Rohrreibungszahl vom Rohrdurchmesser bei
gleichbleibender Rohrwandgüte (Rohrrauhigkeit) heraus. Beide Beobachtungen sind zutreffend. Auch die absoluten Werte
von f bewegen sich in der heute akzeptierten Größenordnung, wie ein Vergleich mit dem Diagramm nach Moody zeigt.
Colebrook formuliert hier die Rohrreibungszahl mit den dimensionslosen Größen (Rohrrauhigkeit/Durchmesser) und Reynoldszahl.
 Diagramm nach Moody
Die Arbeiten insbesondere von Navier, Stokes, Hagen, Poiseuille, Reynolds, Karman, Prandtl und Colebrook führten zur
Formulierung und Darstellung der Rohrreibungszahl f, wie wir sie heute kennen (Diagramm nach Moody). Sie erfasst
die Entwicklung der Rohrreibungszahl aller newtonschen Flüssigkeiten von der laminaren bis zur vollständig
turbulenten Rohrströmung.
Diagramm nach Moody
Die Arbeiten insbesondere von Navier, Stokes, Hagen, Poiseuille, Reynolds, Karman, Prandtl und Colebrook führten zur
Formulierung und Darstellung der Rohrreibungszahl f, wie wir sie heute kennen (Diagramm nach Moody). Sie erfasst
die Entwicklung der Rohrreibungszahl aller newtonschen Flüssigkeiten von der laminaren bis zur vollständig
turbulenten Rohrströmung.
Für Re < 2320 (laminare Rohrströmung) wird die Rohrreibungszahl nach Hagen-Poiseuille berechnet:
f = 64 / Re
 Hagen Poiseuille and Couette Flow
Hagen Poiseuille and Couette Flow
Für Re > 2320 (turbulente Rohrströmung) wird die Rohrreibungszahl
nach [Colebrook 1939, Seite 137] berechnet:
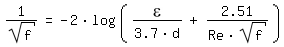
|
Die Beziehung von Colebrook konvergiert für Re => ∞ (vollständig turbulente Strömung) gegen die Beziehung von [Prandtl 1933, Seite 110] nach Kármán:
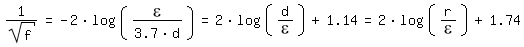
und für ε/d => 0 (glattes Rohr) gegen die Beziehung von [Prandtl 1933, Seite 111]:
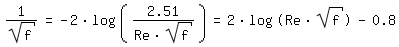
Da laminare Rohrströmung bis Re = 8000 möglich ist
[VDI 1984, Seite Lb1], kann es durch den vorgenannten Rechenweg im kritischen Bereich
(2320 <= Re < 8000) zu einer Überschätzung der Rohrreibungszahl kommen.
Das Moody-Diagramm nach [Moody 1944, Seite 672] ist eine
gelungene Darstellung vorgenannter Gleichungen.
| Literatur |
| [1801 Eytelwein] J.A. Eytelwein, Handbuch der Mechanik fester Körper und der Hydraulik, Berlin bei F.L. Lagarde, 1801 |
| [1804 Prony] R. Prony, Recherches Physico-Mathématiques sur la théorie des eaux courantes, Paris, de L´imprimerie Impériale, 1804 |
| [1822 Navier] M. Navier, Mémoire de l´ Académie des Sciences, Tome 6, 1823, 389 ff |
| [1834 Aubuisson] J.F.Aubuisson de Voisins, Traité D´Hydraulique, Paris, Chez F.G. Levrault, 1834 |
| [1850 Weisbach] J. Weisbach, Lehrbuch der Ingenieur- und Maschinenmechanik, Erster Teil Theoretische Mechanik, 2. Auflage, Braunschweig F. Vieweg und Sohn, 1850 |
| [1858 Darcy] Darcy Mémoire a l´Académie des Sciences, Tome 15, 1858, 141 ff |
| [1883 Osborne Reynolds] Phil. Trans. R. Soc. Lond., 174, 935 ff |
| [1933 Prandtl] L. Prandtl, Neuere Ergebnisse der Turbulenzforschung, Zeitschrift des Vereins Deutscher Ingenieure, Band 77, 1933 |
| [1939 Colebrook] C.F. Colebrook, Turbulent Flow in Pipes, with particular reference to the Transition Region between the Smooth and Rough Pipe Laws, Journal of The Institution of Civil Engineers, Volume 11, 1939 |
| [1944 Moody] L.F.Moody, Friction Factors of Pipe Flow, Transactions of the ASME, Volume 66, 1944 |
| [1984 VDI] VDI-Wärmeatlas 4. Auflage 1984 |